Query Processing

---

This note describes the different types of algorithms that can be used for selections in database queries, and also the differences between materialized and pipelined evaluations.

---

Selection Algorithms

In this chapter we will show and explain the several different algorithms that can be used to perform a selection operation on a database.

Important

In this note, we will use the following notations for evaluating time complexity:

$\textbf{t}_{\textbf{s}}$ - Time to perform a seek on the disk
$\textbf{t}_{\textbf{b}}$ - Time to perform a block transfer

File Scan

Family of search algorithms that perform the search directly through the file where data is stored. Here we only have Linear Search.

Linear Search

In this algorithm, we import from disk each block sequentially, and examine the records in each block, to see if they match the selection condition.

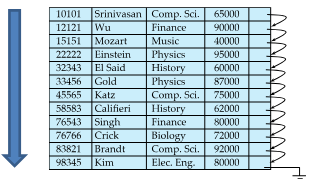
Fig.1: Linear search example

Cost Estimate

• If selection condition is on non-key attribute: $\textbf{t}_{\textbf{s}} + (b \cdot \textbf{t}_{\textbf{b}})$
• If selection condition is on key attribute: $\textbf{t}_{\textbf{s}} + (\dfrac{b \cdot \textbf{t}_{\textbf{b}}}{2})$
  • Search can stop whenever the record is found, because key is unique

Applicability

Linear search can always be applied, regardless of:

• Sorting of the relation
• Selection condition
• Availability of indices

Index Scan

Family of search algorithms that use an index to perform their search. In these are included:

Clustered Index, Equality on Key

In this algorithm, we use a clustered index (order of index = order of file), and that index is on a relation's key; we then simply use the index to find the single record that matches the selection condition.

Cost

Let $\textbf{h}_{\textbf{i}}$ be the height of the B$^+$-tree of the index. The cost is:

$(\textbf{h}_{\textbf{i}} + 1) * (\textbf{t}_\textbf{t} + \textbf{t}_\textbf{s})$

Clustered Index, Equality on Non-Key

Just like the previous algorithm, we use a clustered index, but this time on a non-key attribute, which means that more than one record may be retrieved; therefore we use the index to reach a record that matches the selection condition, and then evaluate the subsequent records, to see if they also match the selection condition; if they do, we add them to the output.

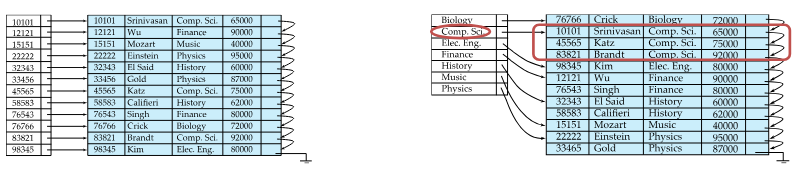
Fig.2: Clustered Index, equality on non-key example

info

Retrieved records will be on consecutive blocks

Cost

Let $\textbf{b}$ be the number of blocks with records that will be added to the final result, and $\textbf{h}_{\textbf{i}}$ the height of the B$^+$-tree of the index. The cost is:

$\textbf{h}_{\textbf{i}} * (\textbf{t}_\textbf{t} + \textbf{t}_\textbf{s}) + \textbf{t}_\textbf{s} + \textbf{t}_\textbf{t} \cdot \textbf{b}$

Non-Clustered Index, Equality on Key/Non-key

We will now see the case of using a non-clustered index to perform our selection; in this case, we will have two scenarios, depending on the attribute used in the selection condition:

• If equality is on key:
  • Search until the (single) correct record is found
• If equality is on non-key:
  • When the correct index entry is found, all the records pointed at by that index entry need to be added to result; this might mean that it is needed to transfer a large number of blocks (if the result of selection is large)

Cost

• If the search-key is unique: $(\textbf{h}_{\textbf{i}} + 1) * (\textbf{t}_\textbf{t} + \textbf{t}_\textbf{s})$
• If the search-key is not unique: $(\textbf{h}_{\textbf{i}} + \textbf{n}) * (\textbf{t}_\textbf{t} + \textbf{t}_\textbf{s})$
  • $\textbf{n}$ is the number of matching records

Selections involving Comparisons

So far we have seen the case of selections using equality conditions; but what if we have selection conditions involving comparisons (e.g., $\ \sigma_{A \le V}(r)$)? We have two options:

1. Use file scan, can be used in any circumstance
2. Make use of indices, with the algorithms that we will show below

Clustered Index with Comparison

When using a clustered index to solve a selection with a comparison condition, we will make use of the fact that the clustered index has the same order has the records' file:

• If $\sigma_{A \ge V}(r)$, we use the index to find the first value $A \ge V$, and retrieve all the subsequent records
• If $\sigma_{A \le V}(r)$, we don't even need to use the index; we just retrieve all records starting from the first, and stop on the first record with $A \ge V$

Non-Clustered Index with Comparison

With non-clustered indices, we cannot simply rely on the fact that the file is ordered on the attribute we want; therefore we will need to use the index to retrieve all valid records.

• For $\sigma_{A \ge V}(r)$, use the index to find the first value $A \ge V$, and then go through each leaf entry, retrieving the records pointed by the pointers.
• For $\sigma_{A \le V}(r)$, start on the first index entry and retrieve the records (using the leaf pointers), until finding $A \gt V$.

Important

This type of search requires an I/O operation per record. This is expensive, and there might be cases it is better to simply use linear scan.

Complex Selections

Conjunction ($\land$)

For selections involving conjunctions, $\Large{\sigma_{\theta1 \ \land \ \theta2 \ \land \ ... \ \theta n}}$, there are three algorithms we can use:

Conjunctive Selection using one Index

In this algorithm, we choose a condition $\theta i$, and use one of the algorithms above that uses an index (all of the algorithms above except linear search) to perform the selection $\Large \sigma_{\theta i}$. We then load the retrieved records, iterate over them and test $\large \theta_{1 \ ... \ n, \ n \neq i}$ in each record, discarding the ones that don't meet the conditions.

Conjunctive Selection using Composite Index

If there exists composite index with the appropriate attributes used in the conditions $\large \theta_{1 \ ... \ n}$, then we can directly use that index to retrieve the valid records.

Conjunctive Selection by Intersection of Identifiers

This algorithm requires that each condition $\large \theta_{1 \ ... \ n}$ has a covering index for the attributes it is testing, and that index must have pointers to records. Then, for each condition, we test the index for that condition, gather all sets of pointers for each condition and then take the interception of all sets of pointers. The result of the select is the records pointed at by the pointers resulting from this interception.

Disjunction ($\lor$)

For disjunction, there are two alternatives. If, for each condition $\large \theta_{1 \ ... \ n}$ in a selection $\Large{\sigma_{\theta1 \ \lor \ \theta2 \ \lor \ ... \ \theta n}}$, there exists a covering index, we can use the following algorithm; otherwise use linear search.

Disjunctive Selection by Union of Identifiers

In this algorithm, we will go through each condition of the disjunction, and get the pointers to the results from that condition using the appropriate index. In the end, we simply take the union of all pointers, and retrieve the records from file.

Negation ($\neg$)

Two alternatives:

• Use linear search
• Transform expression $\large \neg \ \theta$ into $\large \theta'$, and check if there is covering index for $\large \theta'$
  • If there is, use one of the seen algorithms using indices